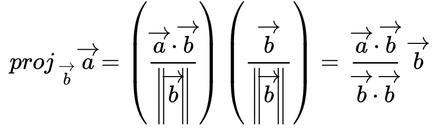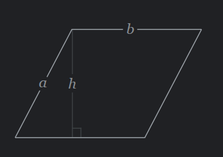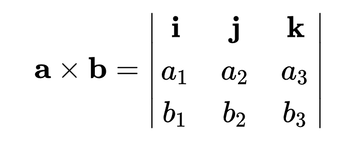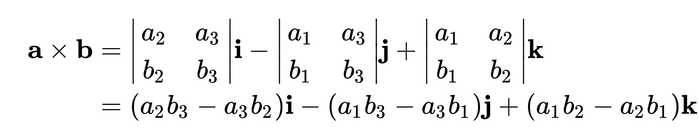Get into GameDev:
cheat-codes for gamedev interviews
━ Maths - Vectors I ━
Introduction
Introducing Vectors
Notation
A vector is a data structure that holds numbers. When typed, a variable that refers to a vector will always be bolded. For example: v. A vector is like a matrix but a vector is always only one column or row. In that sense, a vector is like a very tall or very wide matrix. Vectors are typed in bold and lowercase, matrices are typed in bold and uppercase (like M). Matrices are described as mxn "m by n" where m is the row count and n is the column count. When typed, a vector (like v) always refers to specifically a tall, vertical, one-column vector. In terms of mxn this means n = 1. If we want to refer to a wide vector ( m = 1 ) then we write v^T, this looks like "v to the power of T" but is simply "v transpose". A transpose is a counter-clockwise rotation of a vector.
[ 1 ]
If v = [ 2 ] , then v^T = [ 1 , 2, 3 ].
[ 3 ]
If I write v = [ 1, 2, 3 ], then I am always describing a vertical vector that looks exactly like the v shown on the line above but I am just writing it horizontally for practicality. If a vector is actually horizontal (wide) then I will always use the transpose notation. Now let's explore the significance of a vector with respect to lines which may be a structure you feel more familiar with...
Rays, Lines, Line Segment, and Vector Formulas
A line is a 2D structure that has zero width, zero height, and infinite length. In school you may have learned the line equation y = mx + b. We will not use this equation, it is a very constrained 2D representation of a line that will not be useful for game dev where most of our applications are in 3D. Instead, I want you to think of a line as a container in 3D space. Our line formula is an equation that defines which points in the 3D line within our line. In that regard, it is also a test to see if any given point is on our line. A line contains an infinite amount of points, but two points are sufficient to define the line. If we have two points v1 and v2 we can subtract them to get the direction between them, v (this is a vector). Our line formula is defined using this v in addition to our of the points on the line which we call P (it can be v1, v2, or any other point on the line).
L = P + ( t * v )
The formula above defines line L, starting from point P, into the direction v which is scaled by scalar t. Because a line extends in two directions, t can be negative. Because a line is infinite, t can be any value from -infinity to +infinity. Now here is the cool part... this is also the equation for a direction vector and a line segment. The only difference is that the data type defines the range of our scalar, t. Below are the parametric equations for each of these structures, so-called "parametric" because they all rely on that input parameter t.
L = P + ( t * v ) is a line if t = [ -infinity, +infinity ]
L = P + ( t * v ) is a ray if t = [ 0, +infinity ]
L = P + ( t * v ) is a line segment if t = [ 0, n ]
L = t * v is a vector t = [ -infinity, +infinity ] ( vectors have a magnitude and a direction but no position )
The realization that we can think of direction vectors and line segments as just lines with bounds is a critical insight. Most of the problems we will face with these data types are much easier if we instead solve the problem with lines. For example, we will later explore the problem: "does line segment L intersect plane P?", the solution is basically to first solve "does line L' intersect plane P?" and if it does, then we just need to check if the intersection between L' and P is on line segment L.
A vector is a data structure that holds numbers. When typed, a variable that refers to a vector will always be bolded. For example: v. A vector is like a matrix but a vector is always only one column or row. In that sense, a vector is like a very tall or very wide matrix. Vectors are typed in bold and lowercase, matrices are typed in bold and uppercase (like M). Matrices are described as mxn "m by n" where m is the row count and n is the column count. When typed, a vector (like v) always refers to specifically a tall, vertical, one-column vector. In terms of mxn this means n = 1. If we want to refer to a wide vector ( m = 1 ) then we write v^T, this looks like "v to the power of T" but is simply "v transpose". A transpose is a counter-clockwise rotation of a vector.
[ 1 ]
If v = [ 2 ] , then v^T = [ 1 , 2, 3 ].
[ 3 ]
If I write v = [ 1, 2, 3 ], then I am always describing a vertical vector that looks exactly like the v shown on the line above but I am just writing it horizontally for practicality. If a vector is actually horizontal (wide) then I will always use the transpose notation. Now let's explore the significance of a vector with respect to lines which may be a structure you feel more familiar with...
Rays, Lines, Line Segment, and Vector Formulas
A line is a 2D structure that has zero width, zero height, and infinite length. In school you may have learned the line equation y = mx + b. We will not use this equation, it is a very constrained 2D representation of a line that will not be useful for game dev where most of our applications are in 3D. Instead, I want you to think of a line as a container in 3D space. Our line formula is an equation that defines which points in the 3D line within our line. In that regard, it is also a test to see if any given point is on our line. A line contains an infinite amount of points, but two points are sufficient to define the line. If we have two points v1 and v2 we can subtract them to get the direction between them, v (this is a vector). Our line formula is defined using this v in addition to our of the points on the line which we call P (it can be v1, v2, or any other point on the line).
L = P + ( t * v )
The formula above defines line L, starting from point P, into the direction v which is scaled by scalar t. Because a line extends in two directions, t can be negative. Because a line is infinite, t can be any value from -infinity to +infinity. Now here is the cool part... this is also the equation for a direction vector and a line segment. The only difference is that the data type defines the range of our scalar, t. Below are the parametric equations for each of these structures, so-called "parametric" because they all rely on that input parameter t.
L = P + ( t * v ) is a line if t = [ -infinity, +infinity ]
L = P + ( t * v ) is a ray if t = [ 0, +infinity ]
L = P + ( t * v ) is a line segment if t = [ 0, n ]
L = t * v is a vector t = [ -infinity, +infinity ] ( vectors have a magnitude and a direction but no position )
The realization that we can think of direction vectors and line segments as just lines with bounds is a critical insight. Most of the problems we will face with these data types are much easier if we instead solve the problem with lines. For example, we will later explore the problem: "does line segment L intersect plane P?", the solution is basically to first solve "does line L' intersect plane P?" and if it does, then we just need to check if the intersection between L' and P is on line segment L.
Practice Question: What is the equation of a line that contains these two points: ( 11, 13, 17 ) and ( 10, 11, 14 )?
First, define the direction vector of the line which is the difference of two points within the line.
v = ( 11, 13, 17 ) - ( 10, 11, 14 ) = [ 1, 2, 3 ]
Then define the line as a starting point plus the direction vector scaled by t (a variable scalar).
L = P + ( t * v ) --> L = ( 11, 13, 17 ) + ( t * [ 1, 2, 3 ] )
v = ( 11, 13, 17 ) - ( 10, 11, 14 ) = [ 1, 2, 3 ]
Then define the line as a starting point plus the direction vector scaled by t (a variable scalar).
L = P + ( t * v ) --> L = ( 11, 13, 17 ) + ( t * [ 1, 2, 3 ] )
3D Shapes from 2D Vectors
Above we discussed how the line's equation is something like a test to see if a point is in a 2D line. Abstracting that idea a bit... a group of vectors when considered together are sort of like a formula themselves. For example, a plane is 2D structure that can be defined by two vectors. Any two vectors will work as long as they are not coincident aka collinear aka in the same direction. We'll explore planes in far greater depth later, but the key insight here is that vectors can be thought of as equations of points and so too can planes be though of as equations of vectors. Now let's take that one step further into 3D...
Basis Vectors
A basis is a collection of vectors that can be combined in order to reach any point within a space. Here's anexample:
av + bu = P
If 2D vectors v and u can be combined and scaled to express any 2D point P, then v and u form a basis for R2 (which means 2D space).
- For example let's say P = [ 1, 10], v = [1, 0], and u = [0, 1]. Then the equation can be completed with a = 1 and b = 10.
- But if P = [ 1, 10], v = [1, 0], and u = [2, 0]. Then the equation can never be completed because the second term of P, 10, can never be reached by the equation a*0 + b*0 = 10. There are no values for a or b that can overcome the zero scalar to reach 10.
Practice Question: Which of the following are a basis in their respective dimensions?
- 3 disjoint vectors in R4
- 2 collinear vectors in R3
- [ 0, 1 ], [ 0, 2 ], and [ 5, 1 ]
3 disjoint vectors in R4:
- These vectors are disjoint, that's important! But we need 4 to form a basis in R4.
2 collinear vectors in R3:
- These vectors are on the same line, they alone cannot form a basis.
- Additionally we would need at least three vectors to form a basis in R3.
[ 0, 1 ], [ 0, 2 ], and [ 5, 1 ]:
- Here we have three vectors in R2. The first two are colinear but the third is not.
- So if we take the third and either of the first two...
- ...then we have two disjoint vectors in R2 which is sufficient to form a basis.
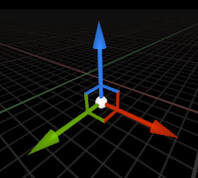
Bases are really important in game development. An object's "transform" is a basis that defines its orientation. Have you ever seen an image like the one below? This is commonly how transforms are visualized. As you can see, there are three disjoint vectors shown. All of a transform's basis vectors are perpendicular.
Vectors for Distance
In addition to defining 3D objects, vectors are commonly used to define the space between objects. In an earlier example we discussed how if you take two points on a line: v1 and v2, then you can subtract them to derive the direction of the line. The order of the points in the subtraction ( "v1 - v2" vs "v2 - v1" ) doesn't matter for a line because it is infinite in both directions, but it matters a lot when directionality is relevant. For example if S is a race's start position and E is the race's position, how do you derive the direction from the start to the end of the race? It's E - S. You always put the end point as the first argument. A pneumonic for this can be "keep your eye on the price" or "put the destination first". It's easy to derive in a 1D case, just consider if you want to get from value 0 to value 10 do you need "10 - 0 = +10" or "0 - 10 = -10" of course we need +10 to get from 0 to 10, as -10 would send us in the wrong direction into negative numbers.
Vector Norms
The magnitude of a vector is the total distance it represents. The vector magnitude is also known as the "L2-norm", "Euclidean norm", or simply "the norm". For 1D vectors, the magnitude is just the value's absolute value. And just like an absolute value for an integer is written with vertical bars, a vector norm is also written this way. An absolute values are only relevant in 1D (basic numbers), but a vector norm is like an absolute value formula that can be applied for higher dimensions. To acknowledge this, some authors will use one line on the sides for absolute value "|x|" and two lines for the vector norm "||x||", but I am not going to do that. For higher dimensional vectors we have a formula to help us out:
|v| = sqrt( ( v.x * v.x ) + ( v.y * v.y ) + ... )
This norm (the Euclidean norm) is the most common kind of norm which is why people sometimes just call it "the norm". But there are actually many kinds of norms. One kind of norm is called the p-norm which takes a variable "p" into an equation. The L2-norm is simply the p-norm with p = 2. You probably won't come across the other norms in game dev.
In addition to defining 3D objects, vectors are commonly used to define the space between objects. In an earlier example we discussed how if you take two points on a line: v1 and v2, then you can subtract them to derive the direction of the line. The order of the points in the subtraction ( "v1 - v2" vs "v2 - v1" ) doesn't matter for a line because it is infinite in both directions, but it matters a lot when directionality is relevant. For example if S is a race's start position and E is the race's position, how do you derive the direction from the start to the end of the race? It's E - S. You always put the end point as the first argument. A pneumonic for this can be "keep your eye on the price" or "put the destination first". It's easy to derive in a 1D case, just consider if you want to get from value 0 to value 10 do you need "10 - 0 = +10" or "0 - 10 = -10" of course we need +10 to get from 0 to 10, as -10 would send us in the wrong direction into negative numbers.
Vector Norms
The magnitude of a vector is the total distance it represents. The vector magnitude is also known as the "L2-norm", "Euclidean norm", or simply "the norm". For 1D vectors, the magnitude is just the value's absolute value. And just like an absolute value for an integer is written with vertical bars, a vector norm is also written this way. An absolute values are only relevant in 1D (basic numbers), but a vector norm is like an absolute value formula that can be applied for higher dimensions. To acknowledge this, some authors will use one line on the sides for absolute value "|x|" and two lines for the vector norm "||x||", but I am not going to do that. For higher dimensional vectors we have a formula to help us out:
|v| = sqrt( ( v.x * v.x ) + ( v.y * v.y ) + ... )
This norm (the Euclidean norm) is the most common kind of norm which is why people sometimes just call it "the norm". But there are actually many kinds of norms. One kind of norm is called the p-norm which takes a variable "p" into an equation. The L2-norm is simply the p-norm with p = 2. You probably won't come across the other norms in game dev.
Practice Question: What is the magnitude of vector v, where v = [ 2, 3, 4 ]?
|v| = sqrt( ( v.x * v.x ) + ( v.y * v.y ) + ( v.z * v.z ) )
|v| = sqrt( ( 2 * 2 ) + ( 3 * 3 ) + ( 4 * 4 ) )
|v| = sqrt( ( 4) + ( 9 ) + ( 16 ) )
|v| = sqrt( 29 )
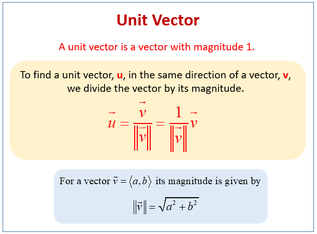
Normalizing Vectors
Often, we don't care at all about the magnitude of a vector and instead would prefer to normalize aka "unitize" it which means scale it to be a length of 1. We do this when we want a vector only for it's direction or if we want to simplify a formula that requires us to use the vector's magnitude as a factor (if we magnitude is 1 then the factor can be removed). To normalize a vector, divide each term by the vector's magnitude. If a vector is normalized, then it will be italicized.
Syntax Key: x<--scalar v<--vector u<--normalized vector M<--matrix P<--point PS<--line (or line segment) defined by points P and S
Practice Question: Convert vector v, where v = [ 2, 3, 4 ], into a unit vector u.
|v| = sqrt( 29 ) <-- (see previous problem)
u = v / |v|
u = [ 2, 3, 4 ] / sqrt( 29 )
u = [ 2 / sqrt( 29 ), 3 / sqrt( 29 ), 4 / sqrt( 29 ) ]
Dot Product
Congratulations, you have made it to the most important section of this entire guide. The dot product aka "the inner product" is absolutely the most common interview topic out of all possible game programming questions. I have never experienced a gameplay engineer interview that has not touched upon the dot product. It is imperative that you learn this topic inside-and-out, upside-down, and sideways. It is ESSENTIAL!
Dot Product: “the product of two vector magnitudes multiplied by the cosine of the angle between the vectors.”
Its primary uses are to find the angle between two vectors and to perform vector projections. To remember that cosine needs to be used for the dot product, I suggest the pneumonic of observing that the ‘o’ and ‘c’ in cosine looks like a dot.
The dot product requires O(n) FLOPs to compute which is pretty fast compared to the cross product.
The dot product can be expressed in many ways, each formula has it's own uses. Here are some common expressions followed by explanations and greater context on their significance. However it does require a horizontal add-an operation that SIMD units cannot do, this makes them repeated dot products slow. One optimization we can do, if you have to do multiple dot products with the same vector v, is to put the unique vectors (for example: x, y, z) into the rows of a matrix and multiply the vector v times the matrix. This yields the three results at the cost of only one horizontal add. I've never done this optimization personally, but I want you to be familiar with some of the tricks like this that we will use in practice for optimization.
a • b = |a| |b| cos( θ )
The most common dot product expression. You must have this memorized. We can use the arccos() function on both sides to pull out the theta angle which represents the angle between vectors a and b. If a and b are of unit length, aka "unit vectors", then their magnitudes are 1 and those factors (|a| and |b| ) can be removed to simplify the formula to acos( a • b ) = θ. The theta we receive from a dot product formula is unsigned meaning it does not have any directionality. So if you have two vectors, the dot product can tell you how much to rotate the first for it to align with the second but you won't know which direction to turn. We will later explore the cross product which does provide that directionality.
a • b = cos( θ )
If both a and b are normal vectors (that means they are of unit length) then the formula can be simplified to the form above. I have a riddle for you: if a • b in this formula result in a negative number, then what does this tell us about the angle θ? Think about the unit circle. Cos is the x value of the angle. And it is only negative if the angle is in the top left or bottom left quadrant of the unity circle. Therefore a negative number on the left hand side of this equation means that that θ is obtuse. Now what if the angle is acute? We then the left hand side value will always be positive. But unlike in the negative case, a positive left hand side value does not mean the angle is always acute since a very obtuse angle in the bottom right quadrant of the unit circle will have a positive Cos. In the next formula we will abstract these observations for any vectors, not just normalized ones.
x • y = 0 if x ⟂ y
When you complete a dot product, if the result is zero then that means the vectors are perpendicular aka orthogonal (regardless of if the vectors are normalized). This is the easiest way to check if vectors are perpendicular. I'd like to combine this insight with the previous equations insights to present you with the following statements which we can use to interpret the result of any dot product.
a • b = |a| |b| if they’re exactly same direction
a • b > 0 separated by an acute angle
a • b = 0 if perpendicular
a • b < 0 separated by an obtuse angle
a • b = -1 |a| |b| if they’re exactly opposite direction
a • b = a b^T = ( a.x * b.x ) + ( a.y b.y )
This formula show that we compute the dot product via the summation of pairwise multiplication of two vectors' components. Vectors are mx1 matrices as as we discussed in the previous chapter, mxn matrices cannot be multiplies unless the n of the first factor equals the n of the second factor. So you cannot multiply two vectors because you can't multiply an mx1 by mx1, when m != 1. However if we transpose the second vector, it becomes 1xm and now we can multiply an mx1 x 1xm because the 1's meet in the middle. This is effectively what the dot product does: it transposes the second vector and then represents basic matrix multiplication. You may notice that in the expanded expression, on the far right, that this looks very similar to the vector norm formula, except there is no square root and we have two distinct vectors. We will explore that similarity in the next formula.
a • a = |a| |a| = sqrt( ( a.x * a.x ) + (a.y * a.y) )^2 = ( a.x * a.x ) + (a.y * a.y)
This formula shows that a vector dotted with itself is equal to it's magnitude squared. This basically amounts to the vector norm formula but the square cancels out the square root.
Dot Product: “the product of two vector magnitudes multiplied by the cosine of the angle between the vectors.”
Its primary uses are to find the angle between two vectors and to perform vector projections. To remember that cosine needs to be used for the dot product, I suggest the pneumonic of observing that the ‘o’ and ‘c’ in cosine looks like a dot.
The dot product requires O(n) FLOPs to compute which is pretty fast compared to the cross product.
The dot product can be expressed in many ways, each formula has it's own uses. Here are some common expressions followed by explanations and greater context on their significance. However it does require a horizontal add-an operation that SIMD units cannot do, this makes them repeated dot products slow. One optimization we can do, if you have to do multiple dot products with the same vector v, is to put the unique vectors (for example: x, y, z) into the rows of a matrix and multiply the vector v times the matrix. This yields the three results at the cost of only one horizontal add. I've never done this optimization personally, but I want you to be familiar with some of the tricks like this that we will use in practice for optimization.
a • b = |a| |b| cos( θ )
The most common dot product expression. You must have this memorized. We can use the arccos() function on both sides to pull out the theta angle which represents the angle between vectors a and b. If a and b are of unit length, aka "unit vectors", then their magnitudes are 1 and those factors (|a| and |b| ) can be removed to simplify the formula to acos( a • b ) = θ. The theta we receive from a dot product formula is unsigned meaning it does not have any directionality. So if you have two vectors, the dot product can tell you how much to rotate the first for it to align with the second but you won't know which direction to turn. We will later explore the cross product which does provide that directionality.
a • b = cos( θ )
If both a and b are normal vectors (that means they are of unit length) then the formula can be simplified to the form above. I have a riddle for you: if a • b in this formula result in a negative number, then what does this tell us about the angle θ? Think about the unit circle. Cos is the x value of the angle. And it is only negative if the angle is in the top left or bottom left quadrant of the unity circle. Therefore a negative number on the left hand side of this equation means that that θ is obtuse. Now what if the angle is acute? We then the left hand side value will always be positive. But unlike in the negative case, a positive left hand side value does not mean the angle is always acute since a very obtuse angle in the bottom right quadrant of the unit circle will have a positive Cos. In the next formula we will abstract these observations for any vectors, not just normalized ones.
x • y = 0 if x ⟂ y
When you complete a dot product, if the result is zero then that means the vectors are perpendicular aka orthogonal (regardless of if the vectors are normalized). This is the easiest way to check if vectors are perpendicular. I'd like to combine this insight with the previous equations insights to present you with the following statements which we can use to interpret the result of any dot product.
a • b = |a| |b| if they’re exactly same direction
a • b > 0 separated by an acute angle
a • b = 0 if perpendicular
a • b < 0 separated by an obtuse angle
a • b = -1 |a| |b| if they’re exactly opposite direction
a • b = a b^T = ( a.x * b.x ) + ( a.y b.y )
This formula show that we compute the dot product via the summation of pairwise multiplication of two vectors' components. Vectors are mx1 matrices as as we discussed in the previous chapter, mxn matrices cannot be multiplies unless the n of the first factor equals the n of the second factor. So you cannot multiply two vectors because you can't multiply an mx1 by mx1, when m != 1. However if we transpose the second vector, it becomes 1xm and now we can multiply an mx1 x 1xm because the 1's meet in the middle. This is effectively what the dot product does: it transposes the second vector and then represents basic matrix multiplication. You may notice that in the expanded expression, on the far right, that this looks very similar to the vector norm formula, except there is no square root and we have two distinct vectors. We will explore that similarity in the next formula.
a • a = |a| |a| = sqrt( ( a.x * a.x ) + (a.y * a.y) )^2 = ( a.x * a.x ) + (a.y * a.y)
This formula shows that a vector dotted with itself is equal to it's magnitude squared. This basically amounts to the vector norm formula but the square cancels out the square root.
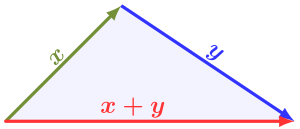
Checkout that cool triangle formed with side lengths of x, y, and z. Triangles have the interesting property that |x + y| <= |x| + |y|. This is called the Triangle Inequality and it means that any one side length of the triangle cannot be greater than the sum of two other side lengths. Think about why this is true, if the red side length was greater than x + y then x and y could not be combine to reach the end of the red arrow and the triangle could not be closed. Now imagine that the sides of the triangle are each vectors. If x, y, and x + y are vectors, then we we can express the following inequality: | x • y | ≤ |x| |y|. This is known as the “Cauchy-Schwarz” inequality and it is a special case of the Triangle Inequality.
Practice Question: Here is a practical guided question on the dot product:
https://www.youtube.com/watch?v=-OKPCMHr7Qc&ab_channel=MatthewVentures
https://www.youtube.com/watch?v=-OKPCMHr7Qc&ab_channel=MatthewVentures
Practice Question: You are given the forward vectors of the player and an enemy: p and e; and the positions of the player and enemy: P and E. Determine if the enemy is facing the player.
This question is a little ambiguous because it doesn't clarify the angle threshold within which two things are considered "facing each other". I'm going to consider the angle between two vectors: the enemy's forward vector and the vector from the enemy to the player. If the angle between those vectors is less than 90 degrees then I would consider them facing each other. We can test this easily with the dot product e • EP = r. If r is negative then we have an angle that is less than 90 degrees and the enemy is therefore facing the player.
Vector Projections
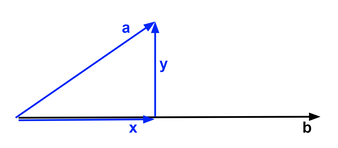
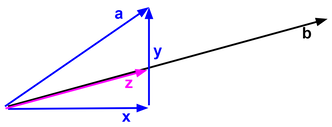
Vector projection is the process of isolating a portion of a vector. Take a look at the image below which shows four vectors: a, b, x, and y. The vector a can actually be broken into two different vectors: x and y. For example y might represent the portion of a that goes in the direction of the y-axis and x might represent the portion of a that goes in the direction of the x-axis. In other words, x and y are component vectors of a. If I asked for the "projection of a onto b" then that would be the same as asking for "the component of a that goes in the direction of b". In this case that would simply be x.
One way that may help you to conceptualize this operation in this example is to think of a sun projecting a shadow of a onto b. Can you imagine how x in the example below is a shadow of a? If not, don't worry about it, the main insight is to realize that of x is the part of a that goes in the direction of b.
One way that may help you to conceptualize this operation in this example is to think of a sun projecting a shadow of a onto b. Can you imagine how x in the example below is a shadow of a? If not, don't worry about it, the main insight is to realize that of x is the part of a that goes in the direction of b.
In this next example, I have changed b. Now the projection of a onto b is z. This is a really important example because it shows that the components of a vector do not need to align with the x-axis or y-axis. You can derive a vector's components in any direction.
Practice Question: In the example above, z is determined to be a component vector of a. Derive w, where w is the remaining component vector of a. Assume we are in a 2D context.
In a 2D context, two non-colinear components together will define a vector. That's because 2 non-colinear vectors form a basis in R2 which can be used to represent any point in that space. Using this insight, we can form the following equation: z + w = a. Just like how x + y = a.
Since w is the remaining part of a, that must means that a = z + w. Therefore w = a - z. But here's something really cool... in this 2D example, if z is a's component in b's direction, then that means w is a's component in the direction perpendicular to b. So just like we were able to project a onto b to get z. If we found some vector perpendicular to b, say c, then the projection of a onto c would be w. This is a 2D case, so a only has two components. But if we were in 3D then we could extrapolate this method further to find a final vector d that would be perpendicular to both b and c and projecting a onto d would give us our third component. Projections are like chopping up our vector into it's composite parts.
Formula: Projection of a onto b
Below is the formula for calculating the projection of "a onto b".
I've written the formula in two ways because I think both have unique utility.
Projections must be onto the origin (Affine Projections)
I want to address a major caveat that caused me to fail an interview some years ago. If projecting onto a structure with position, then that structure needs to contain the origin for the projection to work. This is somewhat complicated, but critical to understand. For example, if you are projecting onto a line, line-segment, or ray, then you need to first translate it to the origin before projecting onto it. Vectors have no position and do not require this step but things like lines, planes, etc. do have position so this step is imperative.
If line segment AB does not go through the origin, here are the steps to projecting vector p onto AB:
1 ) Subtract A from p to obtain p’
2 ) Then project p’ onto AB for partial solution h.
3) Finally, now we add A to h (undoing our offset earlier) for the final answer.
To explain step 1: we needed to subtract any point of AB from p, so A was an easy choice. We could have used B as our offset, any point on AB would have worked. This may seem like a very strange step but basically it is just a walk to the origin. For example, if A = [ 0, 0, 10 ], then it is 10 units up the z-axis away from the origin. By subtracting A from p we are undoing that 10 unit difference. Which then allows us to project onto AB as if AB started at the origin. And finally we just need to undo that translation to convert from our partial solution to a final solution.
Video demonstration: https://youtu.be/eAmwF4oc3DA
Discussion:
Perpendicular Projection
In the projection examples we have thus far discussed, the projection of a onto b resulted in a vector representing the component of a that was parallel to b. In other words, the result of the projection of a onto b is always a vector parallel to b; this has led to some folks referring to this projection as the "parallel projection". In contrast, you might come across something called a "perpendicular projection" aka "orthogonal projection" in which we actually want the component of a that is perpendicular to b. In R3, this is easy to compute. To find the perpendicular projection of a onto b, simply subtract the parallel projection of a onto b from a. This process removes any part of a that was parallel to b, leaving only the perpendicular parts.
- The one on the left shows that the magnitude of b is used to scale two terms: a • b and b. This is important to realize because if b is a unit vector (meaning that you are projecting onto a unit vector), then the projection of "a onto b" simplifies to simply ( a • b ) b. This form is nice because the left term is a scalar that completely accounts for the magnitude of the resulting vector (including the sign) and the right term is a unit vector that completely accounts for the direction.
- The second formula is nice because it combines the two magnitude into a simple denominator dot product then groups all the scalars together on the left. This is a great way to show that when projecting onto b, we are really just trying to calculate how much to scale b. All of our computation simply amounts to a scaling factor to apply to b.
Projections must be onto the origin (Affine Projections)
I want to address a major caveat that caused me to fail an interview some years ago. If projecting onto a structure with position, then that structure needs to contain the origin for the projection to work. This is somewhat complicated, but critical to understand. For example, if you are projecting onto a line, line-segment, or ray, then you need to first translate it to the origin before projecting onto it. Vectors have no position and do not require this step but things like lines, planes, etc. do have position so this step is imperative.
If line segment AB does not go through the origin, here are the steps to projecting vector p onto AB:
1 ) Subtract A from p to obtain p’
2 ) Then project p’ onto AB for partial solution h.
3) Finally, now we add A to h (undoing our offset earlier) for the final answer.
To explain step 1: we needed to subtract any point of AB from p, so A was an easy choice. We could have used B as our offset, any point on AB would have worked. This may seem like a very strange step but basically it is just a walk to the origin. For example, if A = [ 0, 0, 10 ], then it is 10 units up the z-axis away from the origin. By subtracting A from p we are undoing that 10 unit difference. Which then allows us to project onto AB as if AB started at the origin. And finally we just need to undo that translation to convert from our partial solution to a final solution.
Video demonstration: https://youtu.be/eAmwF4oc3DA
Discussion:
- https://math.stackexchange.com/questions/2397750/orthogonal-projection-of-point-onto-line-not-through-origin#:~:text=Projection%20onto%20a%20line%20that,ways%20to%20build%20this%20matrix.
- https://math.stackexchange.com/questions/2376621/projection-onto-a-plane-that-doesnt-pass-through-the-origin
Perpendicular Projection
In the projection examples we have thus far discussed, the projection of a onto b resulted in a vector representing the component of a that was parallel to b. In other words, the result of the projection of a onto b is always a vector parallel to b; this has led to some folks referring to this projection as the "parallel projection". In contrast, you might come across something called a "perpendicular projection" aka "orthogonal projection" in which we actually want the component of a that is perpendicular to b. In R3, this is easy to compute. To find the perpendicular projection of a onto b, simply subtract the parallel projection of a onto b from a. This process removes any part of a that was parallel to b, leaving only the perpendicular parts.
Dot Product Inequality
The dot product inequality is another peculiar and extremely useful application of the dot product. Here is the expression:
0 <= ( AB • AM ) <= ( AB • AB )
This expression is true when M, when projected onto line AB, falls between A and B. For example, with reference to the image below...
- If M was to the left of A then ( AB • AM ) < 0 and the first inequality would not be true.
- If M was to the right of B, then ( AB • AM ) > ( AB • AB ) and the second inequality would not be true.
Let's think about why this works... The dot product can represent a projection. The projection formula normally has a denominator that prevents us from expressing such a simplified inequality. But since we are projecting onto AB in both cases of the dot product, those denominators cancel out in a way that allows us to simplify the expression into the form provided. And when you think about M projected onto AB as M'. All this inequality is asking is if M' is between A and B.
- If M' is to the left of A, then AM' will have a 180-degree angle from AB causing a negative dot product result and failing the first inequality.
- If M' is to the right of B, then AM' will have a 0-degree angel from AB, so the dot product will be 1 as we can compare just the magnitudes. Since M' will be further from A than B, the magnitude of ( AB • AM' ) will exceed the magnitude of ( AB • AB ), failing the second inequality.
Practice Question: Project point M onto line segment AB.
Since AB has position we need to first determine the translation represented by AB. This is simply A.
M' = M - A
M' will provide us with a point that puts M into the perspective of AB.
Now we project M' onto AB, the formula is to normalize AB then scale by Dot( M', AB).
The result is our partial solution H, but H needs to now undo the offset we applied to M by adding A back to it.
Here is the full solution:
M' = M - A
n = ( B - A ) / |B - A|
H = Dot( n, M' )
Solution = H + A
Video demonstration: https://youtu.be/eAmwF4oc3DA
3D Cross Product
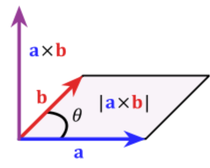
The 3D cross product aka "outer product" or simply "vector product" returns a vector perpendicular to two input vectors, multiplied by the product of their magnitudes, multiplied by the sine of the angle between them. The resulting vector's magnitude is equal to the area of the parallelogram formed by the input vectors. A pneumonic to remember to use the sine function is to think that the ‘s’ in sine looks like two crossed curves.
The 3D cross product formula: a ⨯ b = |a| |b| sin(θ) n
Hey check it out, this formula returns the angle between the two vectors just like the dot product formula, but here it is the sine of the single instead of the cosine of the angle. As you will soon see, a cross product takes a lot of computation, about O(nm) FLOPs, which is much more than the dot product so if you're interested in the angle it makes more sense to just use the dot product. But the directionality of n, can tell us if the angle between input vectors is positive or negative which is not something the dot product can tell us.
Unlike the dot product, which returned a scalar (a number), the cross product returns a vector. In the example below, the purple vector a⨯b is the cross product of vectors a and b. Observe how it is perpendicular to both of them.
The 3D cross product formula: a ⨯ b = |a| |b| sin(θ) n
- n is a unit vector perpendicular to both a and b.
- θ is the angle between a and b.
- If a and b are parallel, then the resulting vector will be the zero vector, 0.
Hey check it out, this formula returns the angle between the two vectors just like the dot product formula, but here it is the sine of the single instead of the cosine of the angle. As you will soon see, a cross product takes a lot of computation, about O(nm) FLOPs, which is much more than the dot product so if you're interested in the angle it makes more sense to just use the dot product. But the directionality of n, can tell us if the angle between input vectors is positive or negative which is not something the dot product can tell us.
Unlike the dot product, which returned a scalar (a number), the cross product returns a vector. In the example below, the purple vector a⨯b is the cross product of vectors a and b. Observe how it is perpendicular to both of them.
Cross Product Magnitude
The above diagram also shows that the volume of the parallelogram formed by a and b is equal to the magnitude of a⨯b. When taking the magnitude of a cross product, remember that n is a unit vector so it can basically be removed from the formula: |a⨯b| = |a| |b| sin(θ).
The above diagram also shows that the volume of the parallelogram formed by a and b is equal to the magnitude of a⨯b. When taking the magnitude of a cross product, remember that n is a unit vector so it can basically be removed from the formula: |a⨯b| = |a| |b| sin(θ).
Practice Question: If you take the cross product of two unit vectors, is the resulting vector going to be unit length?
The magnitude of a cross product of two vectors is equal to the area of a parallelogram formed by two vectors. In which case would a parallelogram has an area of 1? Think of of the formula: area = base * height. For the area to be 1, the base and height would both need to be one as well. The two unit vectors are of length 1 so the answer is yes.
SIKE! Did I fool you? Yes, it is true that area = base * height. But two sides of a parallelogram are not necessarily their base and height. Take a look at the image below, in this case a is not the height, h is! So we need to ask, when is a the same length as h? The answer is only when the parallelogram is a rectangle. So the answer to this question is "the resulting vector will only be unit length if the angle between the input vectors is a right angle".
Cross Product Magnitude Summary
The cross product magnitude |a⨯b| equals...
Cross Product Properties
The cross product is anticommutative: a⨯b = -b⨯a
So basically, when you switch the order of the vectors, one has their sign flipped. If the cross product is going to return the sign of the resulting vector than this makes sense as a required attribute. That's because if you had two input vectors and order did not matter, then crossing both of them would provide you with the the number of degrees between them, but no indication of which direction you would need to turn. The dot product is commutative so we can re-order terms but it alone cannot determine the sign of the angle between them. This trait is one of the things that makes the cross product really useful.
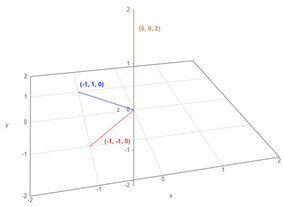
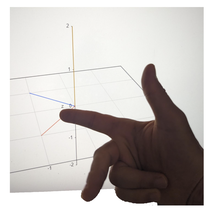
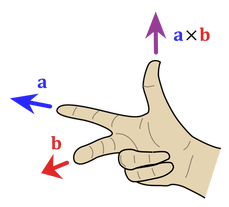
Following up on the cross product's anticommutative-ness, the right-hand rule can be used to determine the direction of the resulting vector. Its a neat little trick where if you use your orient your pointer and middle finger towards each of the input vectors and then your thumb will point in the direction of the cross product result. In the left example below, I have plotted some vectors using an online visualizer.
The blue vector is [-1, -1, 0], the red is [-1, -1, 0], and finally the orange is [0, 0, 2]. The orange vector should be the result of blue vectors crossed with the red vector. In other words, [-1, -1, 0]⨯[-1, -1, 0] = [0, 0, 2]. And check it out, if you aim your pointer finger in the blue direction (to the left), and your middle finger in the red direction (towards you), then your thumb naturally points upwards in the orange direction. See the middle image below.
To demonstrate the anticommutative property, you can now try to switch the order of red and blue. First aim your pointer finger in the red direction (towards you) and now this time aim your middle finger in the blue direction (to the left). In order for your right hand's middle finger to point left, you will need to invert your hand upside down and the result is your thumb will point down instead of up.
The cross product magnitude |a⨯b| equals...
- 0 if the input vectors are parallel. Can you think of why this is? Two colinear lines would result in a parallelogram with zero height! And therefore zero area.
- |a||b| if a ⟂ b, basically this is the same insight from the practice question above. If the two sides of the parallelogram are perpendicular then it will be a rectangle and have area = base * height.
Cross Product Properties
The cross product is anticommutative: a⨯b = -b⨯a
So basically, when you switch the order of the vectors, one has their sign flipped. If the cross product is going to return the sign of the resulting vector than this makes sense as a required attribute. That's because if you had two input vectors and order did not matter, then crossing both of them would provide you with the the number of degrees between them, but no indication of which direction you would need to turn. The dot product is commutative so we can re-order terms but it alone cannot determine the sign of the angle between them. This trait is one of the things that makes the cross product really useful.
Following up on the cross product's anticommutative-ness, the right-hand rule can be used to determine the direction of the resulting vector. Its a neat little trick where if you use your orient your pointer and middle finger towards each of the input vectors and then your thumb will point in the direction of the cross product result. In the left example below, I have plotted some vectors using an online visualizer.
The blue vector is [-1, -1, 0], the red is [-1, -1, 0], and finally the orange is [0, 0, 2]. The orange vector should be the result of blue vectors crossed with the red vector. In other words, [-1, -1, 0]⨯[-1, -1, 0] = [0, 0, 2]. And check it out, if you aim your pointer finger in the blue direction (to the left), and your middle finger in the red direction (towards you), then your thumb naturally points upwards in the orange direction. See the middle image below.
To demonstrate the anticommutative property, you can now try to switch the order of red and blue. First aim your pointer finger in the red direction (towards you) and now this time aim your middle finger in the blue direction (to the left). In order for your right hand's middle finger to point left, you will need to invert your hand upside down and the result is your thumb will point down instead of up.
The cross product is additively distributive ( a ⨯ (b + c)) = ( a ⨯ b ) + ( a ⨯ c)
Remember that the cross product's result vector is perpendicular to the two input vectors. So here we are saying that the cross product of two inputs is going to be the same vector that we would get by combining cross products of one of those input vectors with each of the components of the other input vector.
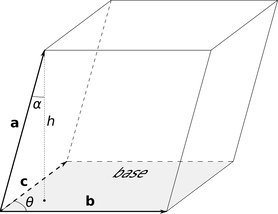
Do you remember how the cross product magnitude is equal to the area of the parallelogram formed by the two input vectors? Well I want to show you something like an abstraction of that into 3D. There's this really cool product called the triple product. It's formed by using the dot product AND the cross product, crazy I know! It looks like this: a • ( b ⨯ c ). And so here is the really cool part, this expression evaluates to the signed volume of the parallelepiped formed by a, b, and c. The below image is an example of such a volume.
Remember that the cross product's result vector is perpendicular to the two input vectors. So here we are saying that the cross product of two inputs is going to be the same vector that we would get by combining cross products of one of those input vectors with each of the components of the other input vector.
Do you remember how the cross product magnitude is equal to the area of the parallelogram formed by the two input vectors? Well I want to show you something like an abstraction of that into 3D. There's this really cool product called the triple product. It's formed by using the dot product AND the cross product, crazy I know! It looks like this: a • ( b ⨯ c ). And so here is the really cool part, this expression evaluates to the signed volume of the parallelepiped formed by a, b, and c. The below image is an example of such a volume.
Cross Product Computation
So far we have discussed at length what cross product represents and what it equals but not how to actually calculate it. In order to calculate it we will need to use the determinant formula covered in the previous chapter. And we will need a new equation. The equation below shows the cross product expressed as a determinant. In this formula, the unit vector variables i, j, and k represent the three components of a 3D vector. When we solve the determinant it simplify to the form: a⨯b = ei + fj + gk. Where i, j, and k are unit vectors and e, f, and g are scalar factors.
So far we have discussed at length what cross product represents and what it equals but not how to actually calculate it. In order to calculate it we will need to use the determinant formula covered in the previous chapter. And we will need a new equation. The equation below shows the cross product expressed as a determinant. In this formula, the unit vector variables i, j, and k represent the three components of a 3D vector. When we solve the determinant it simplify to the form: a⨯b = ei + fj + gk. Where i, j, and k are unit vectors and e, f, and g are scalar factors.
Below is the fully expanded derivation. As you can see, the 3x3 determinant was broken up into three smaller 2x2 determinants. Then the 2x2 determinant formula was used to express a⨯b into the form of a⨯b = ei + fj + gk. Pardon me, I don't have the ability to use subscripts in my text so I will use brackets, hopefully you will understand that in this case e = a[2]*b[3] - a[3]b[2].
Here is the equivalent expansion written in code:
void crossProduct( int v_A[], int v_B[], int c_P[] )
{
c_P[0] = v_A[1] * v_B[2] - v_A[2] * v_B[1];
c_P[1] = -(v_A[0] * v_B[2] - v_A[2] * v_B[0]);
c_P[2] = v_A[0] * v_B[1] - v_A[1] * v_B[0];
}
As you can see, the code is zero-indexed so the index numbers are one less than in the algebraic representation. For example the first multiplication we see is v_A[1] * v_B[2] instead of a[2]*b[3]. As you can see, the cross product requires quite a lot of computation!
void crossProduct( int v_A[], int v_B[], int c_P[] )
{
c_P[0] = v_A[1] * v_B[2] - v_A[2] * v_B[1];
c_P[1] = -(v_A[0] * v_B[2] - v_A[2] * v_B[0]);
c_P[2] = v_A[0] * v_B[1] - v_A[1] * v_B[0];
}
As you can see, the code is zero-indexed so the index numbers are one less than in the algebraic representation. For example the first multiplication we see is v_A[1] * v_B[2] instead of a[2]*b[3]. As you can see, the cross product requires quite a lot of computation!
Practice Question: If given a player's forward vector f and the vector from a player to a target t, explain how you would derive the signed magnitude of the angle the player must turn to that that face the target. Basically, you need to determine how much we need to rotate f so that it is collinear with t and in the same direction as t.
The first part of the problem is to get the angle θ between f and t by using the dot product. That angle is unsigned so we now just need to determine if the rotation is clockwise or counter-clockwise. This second part requires two steps. First we determine the plane we are rotating within. This plane will be defined by the normal vector perpendicular to both f and t. To find that vector we use the cross product: Vector3 planeNormal = Vector3.Cross( characterForward, characterToTarget )
Now to see if our rotation is clockwise from the player's perspective we just need to test if the plane normal is in the same direction as our character's up direction.
bool shouldTurnClockwise = Vector3.Dot( planeNormal, character.up ) > 0; This line works because the dot product returns a positive value only when the input vectors are separated by an acute angle. And if the rotation plane's normal and our player's up are seperated by an acute angle, then that means they point in the same general direction and that means we are rotating clockwise.
Our final answer is that we need to rotate around the plane defined by planeNormal for angle θ in the direction dictated by shouldTurnClockwise.
bool shouldTurnClockwise = Vector3.Dot( planeNormal, character.up ) > 0; This line works because the dot product returns a positive value only when the input vectors are separated by an acute angle. And if the rotation plane's normal and our player's up are seperated by an acute angle, then that means they point in the same general direction and that means we are rotating clockwise.
Our final answer is that we need to rotate around the plane defined by planeNormal for angle θ in the direction dictated by shouldTurnClockwise.
2D Cross Product
In the previous section we learned about the 3D cross product, and you might think that the 2D cross product is the same thing just in 2D. But you'd be wrong! It is true that the 2D cross product takes 2D vectors instead of 3D vectors, but this product returns a scalar instead of a vector. However the 2D cross product has a similar role to the 3D cross product in that it's result will tell us if the first input vector is on the left or right side of the second input vector, just like the 3D cross product can be used to determine the direction of an angle between input vectors.
2D Cross product formulas:
a⨯b = ( a.x * b.y ) - ( b.x * a.y )
AB⨯CD = ( B.x - A.x )( B.y - A.y ) - ( D.x - C.x )( D.y - C.y )
The first formula is for vectors, the second formula is for line segments.
The magnitude of a⨯b is...
2D Cross product formulas:
a⨯b = ( a.x * b.y ) - ( b.x * a.y )
AB⨯CD = ( B.x - A.x )( B.y - A.y ) - ( D.x - C.x )( D.y - C.y )
The first formula is for vectors, the second formula is for line segments.
The magnitude of a⨯b is...
- Positive if the a is on the left hand side of b
- Negative if a is on the right hand side of b
- Zero if a and b are collinear
Practice Question: You are given two points: A and B, and a line segment defined by a start and end points: S and E. Determine if A and B are on the same side of line segment SE.
We can use the 2D cross product to determine what side of a line a point is on. First we test point A. AS ⨯ AE = a. If a < 0, then the point lies on one side of the line, and if a > 0, then it lies on the other side. If a=0, then the point lies exactly on the line. Now we can repeat this step for the other point: B. BS ⨯ BE = b. Now we can compare the results, a and b, to see if they are the same polarity (aka both negative or both positive) which will tell us if A and B are on the same side of SE.
Practice Question: Imagine you are making a 2D game. Given a vector, g, representing the ground plane and a vector, b, pointing to the position of a ball, determine if the ball is above or below the ground.
https://www.youtube.com/watch?v=-n_C7tD55_A&ab_channel=PothOnProgramming
Practice Question: You are given a triangle formed by points ABC. And a separate point, P. Determine if P lies within the triangle.
Basically, to test which side of AB the point P is on, we do AP x AB. If P is on the same side of all the triangle sides then it is in the triangle, so the solution is to just repeat this check for the remaining sides. This approach actually works for all polygons! It just requires you to go through the points in order. Remember the order matters a lot because if you compare a point to AB vs BA those two line segments are literally going in the opposite directions! So make sure to pick a direction (like clockwise) and stick to it such as AB, BC, CA.
Code: https://stackoverflow.com/questions/2049582/how-to-determine-if-a-point-is-in-a-2d-triangle
Thankfully, this is a very common problem and alternative approaches have various benefits/drawbacks. We will discuss a Barycentric coordinate approach in the next chapter. But for completeness I will provide a link to that derivation here in case you're interested: https://www.youtube.com/watch?v=EZXz-uPyCyA&list=PLW3Zl3wyJwWN6V7IEb2BojFYOlgpryp1-&index=7&ab_channel=JorgeRodriguez
Thankfully, this is a very common problem and alternative approaches have various benefits/drawbacks. We will discuss a Barycentric coordinate approach in the next chapter. But for completeness I will provide a link to that derivation here in case you're interested: https://www.youtube.com/watch?v=EZXz-uPyCyA&list=PLW3Zl3wyJwWN6V7IEb2BojFYOlgpryp1-&index=7&ab_channel=JorgeRodriguez