Get into GameDev:
cheat-codes for gamedev interviews
━ Fundamentals ━
Introduction
Bitwise Operators
It seemed to me that the best place to start this guide would be with the very building blocks of all data: bits. Bits are our smallest unit of data and are used to compose all of the larger data types we will discuss later on. A bit is a single number: 0 or 1 aka "off" or "on". Usually when we need a two-state variable we will use a bool (more about those later) but they are 8 bits! So to save space, it is common to instead discretize our bits so that each bit in an 8-bit structure can represent a different parameter's on/off state. When we treat each bit in a data type as its own value, that's called a Bit Field. Now, instead of only two states, we can represent 8*2 states within the same 8-bit structure! And if we consider several bits within a bit field instead of just one at a time ( a process called Bit-Masking ) we can represent many more combinations!
To manipulate a single bit within a bit field, we can use the following operators:
To manipulate a single bit within a bit field, we can use the following operators:
|
|
Bitwise Operations
Let's put these bitwise operators into practice! Below are the most common operations which we may need to perform upon a bitfield.
|
Practice Question: Complete implementations for the following functions...
bool HasAnyFlagSet( int inputFlags, int flagsToCheck ) { }
bool HasAllFlagsSet( int inputFlags, int flagsToCheck ) { }
int EnableFlags( int startingFlags, int flagsToEnable ) { }
int DisableFlags( int startingFlags, int flagsToDisable ) { }
bool HasAnyFlagSet( int inputFlags, int flagsToCheck ) {
return ( inputFlags & flagsToCheck ) != 0;
}
bool HasAllFlagsSet( int inputFlags, int flagsToCheck ) {
return ( inputFlags & flagsToCheck ) == flagsToCheck;
}
int EnableFlags( int startingFlags, int flagsToEnable ) {
return ( startingFlags | flagsToEnable );
}
int DisableFlags( int startingFlags, int flagsToDisable ) {
return ( startingFlags & ~flagsToDisable );
}
Binary / Hexadecimal Numbers
The bits we discussed above have two states ( 0 or 1 ) a number described in bits is called binary ( "bi" meaning two, as in two states ). But you (assuming you are also human) are probably used to numbers in decimal format ( 10 states ). Binary numbers are simply another way of representing decimal numbers and they're specifically an easier format for the computer (composed of binary switches). Another common format is Hexadecimal ( 16 states ), its compactness makes it easier for humans to read. As a video game programmer you will be expected to translate numbers between these formats. You should be very familiar with the following powers of two.
As a mnemonic, I have memorized "2 to the 6 is 64" by singing it out loud to myself like a little jingle. The alliteration of "six" and "sixty-four" makes it a little easy to remember. Memorizing that relationship helps me jump to adjacent powers such as 2^5 with a simple 64/2. The most important one is 2^8 which you should have memorized as 256. This is an incredibly important number because it is the total number of possible numbers which we can represent with an 8-bit value. This is why an unsigned int-8's maximum value is 255 (it would be 256 if we did not also need to represent 0). Using this understanding we can easily calculate the maximum value of an arbitrarily sized integer, let's give it a try!
20 = 1 | 21 = 2 | 22 = 4 | 23 = 8 | 24 = 16 | 25 = 32 | 26 = 64 | 27 = 128 | 28 = 256
Practice Question: What is the value of 2^8 and what is the significance of this value?
If you have 2^8 memorized as 256, that's great. Otherwise I would remember "2^6 is 64" and double that value of 64 twice to reach 256.
The significance of each bits represents the number of unique representations we can create. One bit can be 0 or 1 so a single bit can create two representations (aka 2^1). Two bits can create 2^2 unique representations and so on until 2^8 = 256. So this number 256 is ultimately how many representations a int-8 can take on. And it follows that 255 is the maximum value of an int-8 because the first representation of those potential 256 is used for zero and the rest are for numbers 1-255.
Practice Question: What is the maximum value of a signed int-32?
An unsigned int-32 would have all 32 bits to represent its value, but we need to remember to subtract one because one combination of bits is used to represent 0. Therefore the max value of a uint-32 is 2^32-1.
But I asked for a signed int-32 which requires the first bit to represent the sign. Therefore the max value of a uint-32 is 2^31-1.
Additional reading:
https://stackoverflow.com/questions/94591/what-is-the-maximum-value-for-an-int32
Additional reading:
https://stackoverflow.com/questions/94591/what-is-the-maximum-value-for-an-int32
You may have noticed that I tried to trick you by asking for the signed max instead of the unsigned max. Since we are representing a signed number, we need to divide all possible permutations of our 32 bits into three categories: positives, negatives, and zero. With three categories we cannot evenly divide the permutations. The result is that the absolute value of Int32.MinValue is not equal to the absolute value of Int32.MaxValue. Hopefully that provides you with a hint for the next practice question.
Practice Question: What is the minimum value of a signed int-32?
We learned that the maximum value of a signed int-32 is 2^31-1, because of the 32 bits one needs to be used
for the sign (hence the 31) and because one combination of bits is used to represent 0 (hence the -1). Because
we accounted for 0 by lowering the maximum value by 1, we do not need to constrain the minimum value.
Therefore the minimum value of a signed int-32 is simply -2^31.
Additional reading:
https://stackoverflow.com/questions/11243014/why-the-absolute-value-of-the-max-negative-integer-2147483648-is-still-2147483
Additional reading:
https://stackoverflow.com/questions/11243014/why-the-absolute-value-of-the-max-negative-integer-2147483648-is-still-2147483
We are about to jump into Two's Complement which is the way fixed-point numbers (such as ints and longs) are represented. We will cover binary and hexadecimal approaches but before we do, I want to provide you with this useful list to remind you of how two digit numbers are represented in Hex (this will come in handy very soon!).
Decimal: 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15
Hex: 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F
Positive numbers in binary:
Representing numbers in binary or hex is a simple process of first understanding what exponent each column of the number represents and then calculating the total value in each column. I explain this in detail within the following video.
Two's Complement:
In an interview, it is more likely you will be asked to represent a negative number because that process requires you to understand the positive representation in addition to two more steps. In total, the three steps to writing a negative number in binary or hex are:
- Write the number
- Take the 1's complement
- Add 1
Here are two simple examples that break down the process into those simple steps.
In an interview, it is more likely you will be asked to represent a negative number because that process requires you to understand the positive representation in addition to two more steps. In total, the three steps to writing a negative number in binary or hex are:
- Write the number
- Take the 1's complement
- Add 1
Here are two simple examples that break down the process into those simple steps.
|
“Please write -5 in binary”
Step 1: write 5 (as an int8) 0000 0101 Step 2: take 1’s complement (invert bits) If binary just swap 1’s with 0’s and vice-versa 1111 1010 Step 3: Add 1 (so it’s 2’s complement) 1111 1011 |
“Please write -2 in hex”
Step 1: write 2 (as an int8) 02 Step 2: take 1’s complement For hex, just do |# - 15| or (# + 15)%16 ( ex. the 0’s become F’s) FD (or 1111 1101 in binary) Step 3: Add 1 (so it’s 2’s complement) FE |
Step 2 for hex numbers is normally the hardest part for students because they learn it in the binary example as "simply swap the 1's and 0's" and suddenly that simplification does not apply for hex examples. It may be easier to think of the 1's complement as |#-Max| where # is the current digit and Max is the largest value that digit can hold. This approach works in both cases.
- For example, in binary the Max is 1, so this applied to a 0 will yield: |0-1| --> |-1| --> 1
- And in hex, the max is 15 or "F" (shown in our list above), so this applied to 0 will yield: |0-15| --> |-15| --> 15 or "F"
This approach will always work, whether it's binary, hex, or maybe even octal that we need to convert.
Additional Binary & Hex Notes:
- If asked for HEX_1 - HEX_2, instead do... HEX_1 + ( 2’s complement of HEX_2)
- 0b10000 will declare 16 in binary, the b means binary
- 0x00000010 will declare 16 in hex, the x means hex
- Each hex number is represented using 4 binary bits, hex notation is simple an abbreviation
Misc Numbers Info:
You should be familiar with the ASCII table. Know that it has 127 entries, and know that A is 065
Endianness: this term refers to the order in which a number's bits are stored.
----- Big-Endian = stored starting with most-significant-bytes
---- Little-Endian = stored starting with least-significant-bytes.
---- Note: Little-Endian is the widespread default.
For storage, you should prefer data types that express the exact size such as int_8 instead of the generic int.
In the next section we will discuss an alternative way to represent numbers that will allow for decimal values.
- For example, in binary the Max is 1, so this applied to a 0 will yield: |0-1| --> |-1| --> 1
- And in hex, the max is 15 or "F" (shown in our list above), so this applied to 0 will yield: |0-15| --> |-15| --> 15 or "F"
This approach will always work, whether it's binary, hex, or maybe even octal that we need to convert.
Additional Binary & Hex Notes:
- If asked for HEX_1 - HEX_2, instead do... HEX_1 + ( 2’s complement of HEX_2)
- 0b10000 will declare 16 in binary, the b means binary
- 0x00000010 will declare 16 in hex, the x means hex
- Each hex number is represented using 4 binary bits, hex notation is simple an abbreviation
Misc Numbers Info:
You should be familiar with the ASCII table. Know that it has 127 entries, and know that A is 065
Endianness: this term refers to the order in which a number's bits are stored.
----- Big-Endian = stored starting with most-significant-bytes
---- Little-Endian = stored starting with least-significant-bytes.
---- Note: Little-Endian is the widespread default.
For storage, you should prefer data types that express the exact size such as int_8 instead of the generic int.
In the next section we will discuss an alternative way to represent numbers that will allow for decimal values.
Practice Question: How would you write -42 in hex?
Step 1: Write 42 in hex.
I know that my answer will be a number with several columns. I start by writing out labels for my columns from right to left to assess how many columns I will need. First, 16^0 = 0, then 16^1 = 16. These two columns are respectively the 0's column and the 16's column. I know I will not need more than these 2 columns because the highest value I can place into the 16's column is 15 (F). And 15 * 16 is a value far beyond 42, which means I will not need additional columns to reach the number 42.
To determine which number to put in the 16's column, I divide 42 by 16. The result is 2, with 10 remaining. So I place a 2 in the 16's column and bring the remaining 10 into the 0's column. The 0's column is our final column and we place the entire remainder of 10 inside by using the letter A. Remember that each column can only have one digit, so when we need to represent a two digit number, they become letters (in this case 10-->A).
Our final answer for this step is therefore 2A.
Step 2: take 1's compliment.
In this case we are working in hex, so the 1's compliment is |#-15|. Let's apply this to both column values, 2 and A.
2 : |2-15| = |-13| = 13 = D
A : |A-15| = |10-15| = |-5| = 5
Our final answer for this step is therefore D5.
Step 3: add 1
In this step we add 1 to the entire number (not each column). Our 0's column is currently 5, 5+1=6. 6 does not exceed 15 (the maximum value we can hold in any particular column) so we don't need to worry about carrying over any values to the 16's column.
Our final answer for this step is therefore D6.
I should note that this D6 is represented by 8-bits. If it were instead using a 16-bit representation, then we would have 00D5 as our answer to Step 1, and FFD6 as our answer to Step 3.
I know that my answer will be a number with several columns. I start by writing out labels for my columns from right to left to assess how many columns I will need. First, 16^0 = 0, then 16^1 = 16. These two columns are respectively the 0's column and the 16's column. I know I will not need more than these 2 columns because the highest value I can place into the 16's column is 15 (F). And 15 * 16 is a value far beyond 42, which means I will not need additional columns to reach the number 42.
To determine which number to put in the 16's column, I divide 42 by 16. The result is 2, with 10 remaining. So I place a 2 in the 16's column and bring the remaining 10 into the 0's column. The 0's column is our final column and we place the entire remainder of 10 inside by using the letter A. Remember that each column can only have one digit, so when we need to represent a two digit number, they become letters (in this case 10-->A).
Our final answer for this step is therefore 2A.
Step 2: take 1's compliment.
In this case we are working in hex, so the 1's compliment is |#-15|. Let's apply this to both column values, 2 and A.
2 : |2-15| = |-13| = 13 = D
A : |A-15| = |10-15| = |-5| = 5
Our final answer for this step is therefore D5.
Step 3: add 1
In this step we add 1 to the entire number (not each column). Our 0's column is currently 5, 5+1=6. 6 does not exceed 15 (the maximum value we can hold in any particular column) so we don't need to worry about carrying over any values to the 16's column.
Our final answer for this step is therefore D6.
I should note that this D6 is represented by 8-bits. If it were instead using a 16-bit representation, then we would have 00D5 as our answer to Step 1, and FFD6 as our answer to Step 3.
Floating-Point Numbers
We just explored how Fixed-Point numbers are represented at the bit level. Fixed-Point is great for whole numbers, but when we need to express decimal numbers we use Floating-Point numbers. Floating point numbers have an interesting tradeoff, they can express very large numbers (both negative and positive) but as the magnitude of the numbers increases, it decreases its precision. Here is how a float is laid out in memory:
1 09876543 21098765432109876543210
+-+--------------+---------------------------------------------+
| | +-- 23 significand / mantissa (normal binary #)
| +----------------------------- 8 exponent (128 - value of the exponent)
+-------------------------------------- 1 sign bit (if 1 then it's negative)
An interesting decision was made here. The float's designers chose for the exponent bits to represent a number that would be subtracted from 128 instead of representing the exponent itself. That allows for fractions because a large number subtracted from 128 will yield a negative exponent.
A float's lack of precision at large magnitude's is its general downside. This was a big problem for Minecraft, dubbed the Far Lands. In God of War, the team resolved this issue by introducing intermediary transforms for the level sections so that at any given time you only need to make calculations relative to a somewhat-nearby origin (so the numbers never got too big). In Star Citizen, the team used double precision floating point values (these "double floats" are implemented like floats but they're double the size). I think the latter approach is extraordinarily rare, developers usually avoid doubles because they take up so much space. In the next sections we will explore the relative sizes of these objects and the consequences they have on memory layout.
It's important to understand that floats are not uniformly spread out, their available representations are super dense around zero and then spread out more and more as magnitude increases. Take a look at the graphic below which illustrates the density of possible floats.
1 09876543 21098765432109876543210
+-+--------------+---------------------------------------------+
| | +-- 23 significand / mantissa (normal binary #)
| +----------------------------- 8 exponent (128 - value of the exponent)
+-------------------------------------- 1 sign bit (if 1 then it's negative)
An interesting decision was made here. The float's designers chose for the exponent bits to represent a number that would be subtracted from 128 instead of representing the exponent itself. That allows for fractions because a large number subtracted from 128 will yield a negative exponent.
A float's lack of precision at large magnitude's is its general downside. This was a big problem for Minecraft, dubbed the Far Lands. In God of War, the team resolved this issue by introducing intermediary transforms for the level sections so that at any given time you only need to make calculations relative to a somewhat-nearby origin (so the numbers never got too big). In Star Citizen, the team used double precision floating point values (these "double floats" are implemented like floats but they're double the size). I think the latter approach is extraordinarily rare, developers usually avoid doubles because they take up so much space. In the next sections we will explore the relative sizes of these objects and the consequences they have on memory layout.
It's important to understand that floats are not uniformly spread out, their available representations are super dense around zero and then spread out more and more as magnitude increases. Take a look at the graphic below which illustrates the density of possible floats.
There is a line for each possible float, and wow there are so many near zero you can't even discern individual lines. But As we near 1 the values are already spreading out. They will be much further apart when we get to higher numbers. Number that cannot be represented are called denormals and numbers below the minimum number we can represent are called subnormals. How can we deal with these limitations?
If you are dealing with small and big numbers, make sure to deal with your big numbers first. For example, try to determine which of these will be more accurate (assume positive float values).
Big + small - Big OR Big - Big + small
The second option is better because by subtracting the big numbers first we will have a smaller sum to add with our small number. If you have a very big number and a very small number adding them may not change the big number at all! So we want to avoid that.
Ultimately, we can't avoid float inaccuracy and we need to be extra safe with checking if numbers are not quite the same but they should be. Most coders will use functions like IsNearlyEqual and IsNearlyZero to check if a value is close enough to the comparison value. Let's try to implement one of those values together
Discuss how adding big numbers with small numbers can lead to loss of data and how to approach fixes to this phenomenon. Include mention of IsNearlyEqual and IsNearlyZero. Include a practice question to code a method such as IsNearlyEqual. Explain the role of subnormal numbers aka denormals.
If you are dealing with small and big numbers, make sure to deal with your big numbers first. For example, try to determine which of these will be more accurate (assume positive float values).
Big + small - Big OR Big - Big + small
The second option is better because by subtracting the big numbers first we will have a smaller sum to add with our small number. If you have a very big number and a very small number adding them may not change the big number at all! So we want to avoid that.
Ultimately, we can't avoid float inaccuracy and we need to be extra safe with checking if numbers are not quite the same but they should be. Most coders will use functions like IsNearlyEqual and IsNearlyZero to check if a value is close enough to the comparison value. Let's try to implement one of those values together
Discuss how adding big numbers with small numbers can lead to loss of data and how to approach fixes to this phenomenon. Include mention of IsNearlyEqual and IsNearlyZero. Include a practice question to code a method such as IsNearlyEqual. Explain the role of subnormal numbers aka denormals.
Practice Question: Implement the function IsNearlyEqual.
bool IsNearlyEqual( float a, float b ) { /* TODO */ }
Nothing too fancy here, our solution is to simply check if the difference of the values is below an acceptable threshold which will vary based on the use case.
bool IsNearlyEqual( float a, float b ) {
return abs( a - b ) < 0.01f;
}
Practice Question: What's the fastest way to tell if 2 signed floats are the same polarity?
Compare the sign bit of both numbers to see if they are equal, an AND or XOR would work. Here's a walkthrough on how we can use our operators to compare the sign bit...
The float's first (leftmost) bit is a sign bit. To learn more about float checkout the below section "Floating-Point Numbers". So now that we know we need to compare the first bit of the numbers to see if they are equal, let's think through how we can most efficiently compare the first bits of both numbers.
Let's walk through our bitwise operators to see if any of them can help us here... What if we try AND? If you AND two numbers then the resulting value's ith bit will be 1 if the ith bits of both input numbers was 1. For example 1001 AND 1100 = 1000. So if we AND our numbers then we can just check the first bit of the result to see if it is a 1. It will be a 1 if both of the input values were 1. But this approach wouldn't quite work to check if the two input values were both 0. That's because if both of the input values had a 0 as their first bit, the resulting value's first bit would be 0 which would be indistinguishable from a 0 we would get if the two input values had different values as their first bit. Put a bit more simply... since 0 & 0 = 0 and 0 & 1 = 0. We can't tell which case the 0 came from.
What about if we use XOR? If you XOR two numbers then the resulting value's ith bit will be 1 if the ith bits of both input numbers are not the same value. For example 1001 XOR 1100 = 0101. So if we XOR our numbers then we can just check the first bit of the result to see if it is a 1. It will be a 1 if the input values had different values in their ith bit. This is exactly what we need! If the resulting value of a XOR has a 1 in the first bit then that means the two values had different values in their ith bit meaning they are of different polarity. So the solution is to XOR the two values, then check the first bit to see if it is 0 which would mean that the two input values had the same sign bit. Try it out with some examples to test.
The float's first (leftmost) bit is a sign bit. To learn more about float checkout the below section "Floating-Point Numbers". So now that we know we need to compare the first bit of the numbers to see if they are equal, let's think through how we can most efficiently compare the first bits of both numbers.
Let's walk through our bitwise operators to see if any of them can help us here... What if we try AND? If you AND two numbers then the resulting value's ith bit will be 1 if the ith bits of both input numbers was 1. For example 1001 AND 1100 = 1000. So if we AND our numbers then we can just check the first bit of the result to see if it is a 1. It will be a 1 if both of the input values were 1. But this approach wouldn't quite work to check if the two input values were both 0. That's because if both of the input values had a 0 as their first bit, the resulting value's first bit would be 0 which would be indistinguishable from a 0 we would get if the two input values had different values as their first bit. Put a bit more simply... since 0 & 0 = 0 and 0 & 1 = 0. We can't tell which case the 0 came from.
What about if we use XOR? If you XOR two numbers then the resulting value's ith bit will be 1 if the ith bits of both input numbers are not the same value. For example 1001 XOR 1100 = 0101. So if we XOR our numbers then we can just check the first bit of the result to see if it is a 1. It will be a 1 if the input values had different values in their ith bit. This is exactly what we need! If the resulting value of a XOR has a 1 in the first bit then that means the two values had different values in their ith bit meaning they are of different polarity. So the solution is to XOR the two values, then check the first bit to see if it is 0 which would mean that the two input values had the same sign bit. Try it out with some examples to test.
Data Type Sizes
Before we get started talking about data types, you should know the following conversions.
Now we are ready to begin covering the memory footprints of several common data types. In an interview, candidates will be expected to recite these values from memory. Note that 1 byte = 8 bits. Also note that the size of several of these types varies depending on if the processor size (32-bit vs 64-bit). However, since the first PlayStation, pretty much all development has been focused on 64-bit processors. More historical context here.
- 1 TB = 1000 GB
- 1 GB = 1000 MB
- 1 MB = 1000 KiB
- 1 KiB = 1000 B
- 1 B = 8 bits
Now we are ready to begin covering the memory footprints of several common data types. In an interview, candidates will be expected to recite these values from memory. Note that 1 byte = 8 bits. Also note that the size of several of these types varies depending on if the processor size (32-bit vs 64-bit). However, since the first PlayStation, pretty much all development has been focused on 64-bit processors. More historical context here.
Data Type |
32-bit Size |
64-bit Size (if different) |
Representation |
Bool |
1 byte ( 8 bits ) |
- |
- |
Char |
1 byte ( 8 bits ) |
- |
- |
Short |
2 bytes ( 16 bits ) |
- |
- |
Int |
4 bytes ( 32 bits ) |
- |
Two's Complement |
Long |
4 bytes ( 32 bits ) |
8 bytes ( 64 bits ) |
Two's Complement |
Float |
4 bytes ( 32 bits ) |
- |
Floating Point |
Double |
8 bytes ( 64 bits ) |
- |
Floating Point |
Pointer |
4 bytes ( 32 bits ) |
8 bytes ( 64 bits ) |
- |
While an Int is 32 bits by default, we often need to represent a number with a much smaller range. For these cases we can save memory by using a Int type of explicit size such as int8_t which only uses 8 bits. More details here.
Since pointers are used to represent memory addresses, the pointer's size (and therefore it's maximum value) implicitly defines how much memory we can use. A 32-bit pointer can only access values up to about 3.5 GB of RAM (this is a serious limitation), whereas a 64-bit pointer could theoretically access values up to 17 Million GB of RAM.
Below are some game file sizes for perspective. Halo 1 (Combat Evolved) was released on the original Xbox (which was 32-bit) the later entries were released on 64-bit hardware.
Halo 1 (2001) - 1.2 GB
Halo 2 (2004) - 20 GB
Halo 3 (2007) - 55 GB
Halo 4 (2012) - 55 GB
Halo 5 (2015) - 95 GB
Halo ∞ (2021) - 48 GB
Since pointers are used to represent memory addresses, the pointer's size (and therefore it's maximum value) implicitly defines how much memory we can use. A 32-bit pointer can only access values up to about 3.5 GB of RAM (this is a serious limitation), whereas a 64-bit pointer could theoretically access values up to 17 Million GB of RAM.
Below are some game file sizes for perspective. Halo 1 (Combat Evolved) was released on the original Xbox (which was 32-bit) the later entries were released on 64-bit hardware.
Halo 1 (2001) - 1.2 GB
Halo 2 (2004) - 20 GB
Halo 3 (2007) - 55 GB
Halo 4 (2012) - 55 GB
Halo 5 (2015) - 95 GB
Halo ∞ (2021) - 48 GB
Practice Question: How large is an int* on a 64-bit system? What about a float* on a 64-bit system?
Both int* and float* are pointers so they will both be the size of a pointer (we can disregard the int vs float distinction regarding the type of data we are pointing to). A pointer is 8 bytes ( 64 bits ) on a 64-bit system. So both of these will be 8 bytes.
The previous practice question mentioned a "64-bit" system, what does that mean? The 64 refers to the processor's register size and usually specifies the word size as well. A word is the amount of data that can be manipulated at once by a processor. Pretty much all modern processors are 64-bit meaning that the processor can (typically) only work on 64 bits (aka 8 bytes) of data at a time. You may come across the terms halfword and doubleword (aka DWORD) which are simply multiples of that value.
Data Type |
32-bit Size |
64-bit Size |
WORD |
4 bytes ( 32 bits ) |
8 bytes ( 64 bits ) |
DWORD (double word) |
8 bytes ( 64 bits ) |
16 bytes ( 128 bits ) |
QWORD (quadruple word) |
16 bytes ( 128 bits ) |
32 bytes ( 256 bits ) |
Alignment & Padding
With some rare exceptions, the size of a data type also determines an attribute called its "alignment". For example, an Int is 4 bytes large and therefore 4-byte aligned. When data types are stored into memory they are stored at the next available alignment boundary of appropriate size. Let's break that process down with an example. In the diagram below, I marked the 4-byte alignment boundaries with X1, X2, and X3. If we wanted to store an Int at Y1 (position 2) we might instead add bytes of padding at position Y1 and Y2, then we could place the Int at position X2 so that it is aligned. In simple terms, we find the next 4-byte aligned address by determining the next address that is a multiple of 4.
Data: X1 | | Y1 | Y2 | X2 | | | | X3 | |
Address: 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
Aligning data can drastically decrease the time it takes to access it, and some processors actually cannot perform reads on unaligned addresses. In C++, the compiler will automatically align data which can lead to some interesting behavior. For example, take the following struct on the left:
Data: X1 | | Y1 | Y2 | X2 | | | | X3 | |
Address: 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
Aligning data can drastically decrease the time it takes to access it, and some processors actually cannot perform reads on unaligned addresses. In C++, the compiler will automatically align data which can lead to some interesting behavior. For example, take the following struct on the left:
|
struct MixedData{
char Data1; short Data2; int Data3; char Data4; }; |
This struct (on the left) is 8 bytes large prior to compilation:
1byte (char) + 2byte (short) + 4byte (int) + 1byte (char) = 8 bytes However, after compilation, the compiler will add padding to align the data as shown on the right. These additional 4 bytes of padding mean that this struct will actually use 12 bytes of memory. The trailing 3 bytes of padding are due to the struct assuming more MixedData's will be declared after it (as in an array). |
struct MixedData{
char Data1; char Padding1[1]; short Data2; int Data3; char Data4; char Padding2[3]; }; |
Why do 3 bytes of padding follow Data4 in the right-hand-side example? After all, if a MixedData would follow then it would start with a char which does not require a 4-byte alignment. The reason is that most hardware is specifically built for 4-byte alignment. The compiler will pad any struct that is not 4-byte aligned until it is aligned (unless you tell the compiler not to). But 4-bytes is only the minimum, if your struct contains a member type that is aligned to a larger byte count it will align to that instead. For example let's say the struct included an uint64_t (aligned to 8 bytes), then it would have added 5 bytes of padding to reach 8-byte alignment instead of 4-byte alignment.
Source: https://stackoverflow.com/questions/45463701/why-is-the-compiler-adding-padding-to-a-struct-thats-already-4-byte-aligned
To reduce the amount of padding a struct will need, structs should always be laid out with data members in order of descending size. Note that you can explicitly tell a compiler to not add padding by wrapping a struct in: “#pragma pack(push,1)” and “#pragma pack(pop)”. I also want to underscore here that the struct itself does not have a preferred alignment, we are referring to the aligning of each of its data members and not the alignment of the struct itself.
Source: https://stackoverflow.com/questions/45463701/why-is-the-compiler-adding-padding-to-a-struct-thats-already-4-byte-aligned
To reduce the amount of padding a struct will need, structs should always be laid out with data members in order of descending size. Note that you can explicitly tell a compiler to not add padding by wrapping a struct in: “#pragma pack(push,1)” and “#pragma pack(pop)”. I also want to underscore here that the struct itself does not have a preferred alignment, we are referring to the aligning of each of its data members and not the alignment of the struct itself.
Practice Question: What is the optimal way to order the data members of the following struct to reduce padding?
struct MixedData{
char Data1;
short Data2;
int Data3;
char Data4;
};
struct MixedData{
char Data1;
short Data2;
int Data3;
char Data4;
};
Simply order the struct with its data members in decreasing size order.
struct MixedData{
int Data3; <- largest
short Data2; <- medium
char Data1; <- smaller
char Data4; <- small
};
Practice Question: What is the size of the following struct before and after compilation?
struct MixedData{
short Data2;
float Data1;
};
struct MixedData{
short Data2;
float Data1;
};
Prior to compilation the size would be 2bytes (short) + 4bytes (float) = 6bytes.
After compilation, two bytes of padding would be added after the short so that the float will be 4-byte aligned. The resulting size is then 8 bytes.
Additional reading:
https://www.youtube.com/watch?v=c0g3S_2QxWM&list=PLW3Zl3wyJwWPmA00yqu9wiCREj4Of_1F8&index=15&ab_channel=JorgeRodriguez
After compilation, two bytes of padding would be added after the short so that the float will be 4-byte aligned. The resulting size is then 8 bytes.
Additional reading:
https://www.youtube.com/watch?v=c0g3S_2QxWM&list=PLW3Zl3wyJwWPmA00yqu9wiCREj4Of_1F8&index=15&ab_channel=JorgeRodriguez
There are more examples of places where we want to prevent padding. For example, bools have 8 bytes even though they only hold true/false information which in theory only needs one bit's worth of data. In the earlier bitwise operations section, we discussed how a bytes can be used as a bit flag so that different combinations of bits could map to several meanings. If you have 8 bits, each with two potential values ( 0 or 1 ) then you have a total of 2^8 = 256 unique combinations. Though usually we just want to store a true/false value in each bit which is basically eight bools in the same amount of data it would take to store one bool. The C++ compiler actually provides a way to do this (and it is very compiler dependent). We can declare bools like this:
bool myFirstBool : 1;
bool mySecondBool : 1;
The trailing ": 1" means that we should only use one bit for this value. If we have a long list of bools this may lead to great space savings. It can store 8 bool bits into one byte. Some limitations to this approach:
- the compiler may disregard your request
- the data is all sharing an address so if you set a data breakpoint on one it will trigger when another is edited
- writes to bitfields are NOT atomic (they're a read-modify-write) which could cause issues in multithreaded environments. The problem case would be if we have several of these bools (let's say 10 of them). And if two processes try to access the bit field, maybe both will access a word of data (8 bytes) meaning that each will access the same data even if they are trying to change separate bools. This case requires atomics to work correctly, and bitfields aren't atomic.
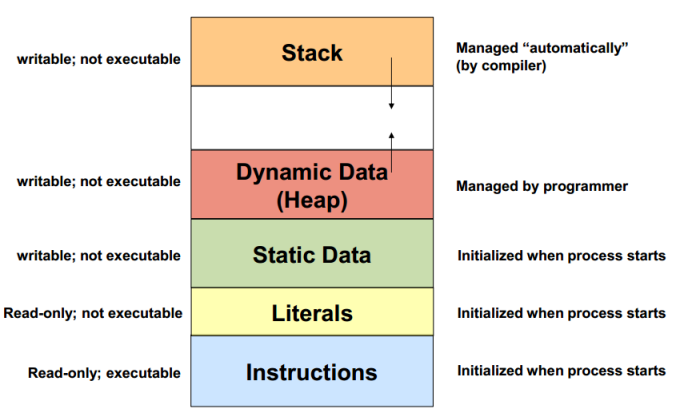
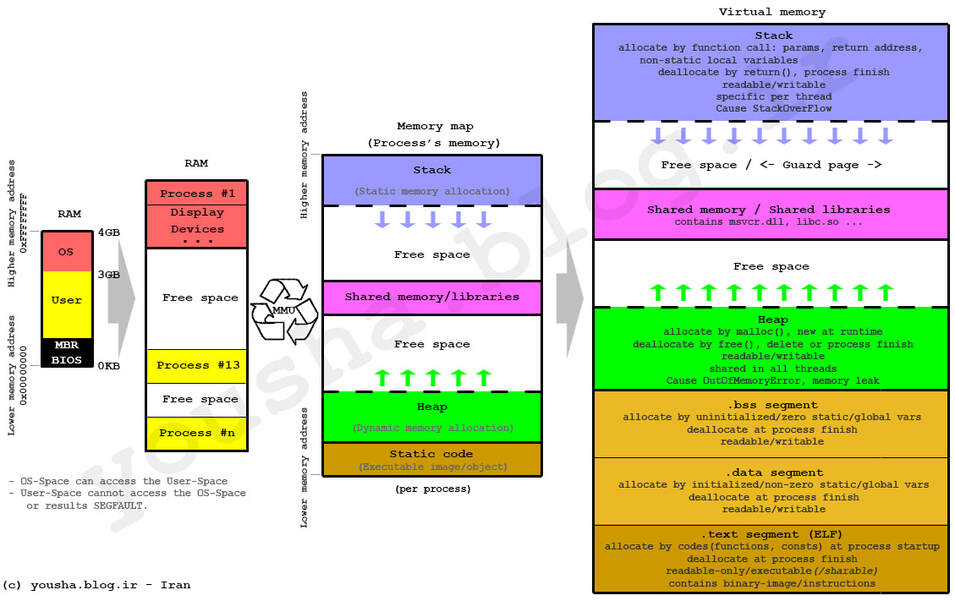
Memory Regions
Memory is stored in different regions based on their usage. You should be aware of the following memory regions and their properties.
|
Stack Region:
|
The more detailed diagram below includes the additional Shared Memory region (between the Stack and Heap) which is used for special "shared memory objects" which represent memory that can be mapped concurrently into the address space of more than one process. Most games are just a single executable (aka only one process) so no sharing is required and this region is irrevelant.
It also splits the Static Data segment into a BSS segment (between the Heap and Data segments) and Data segment, the distinction here being that BSS is for uninitialized global and static objects whereas Data is for initialized global and static objects. A pneumonic for this distinction is that since BSS data is uninitialized, for all we know those data values are just random bullshit. The Data segment is usually further divided into a read-only and read-write section.
It also splits the Static Data segment into a BSS segment (between the Heap and Data segments) and Data segment, the distinction here being that BSS is for uninitialized global and static objects whereas Data is for initialized global and static objects. A pneumonic for this distinction is that since BSS data is uninitialized, for all we know those data values are just random bullshit. The Data segment is usually further divided into a read-only and read-write section.
Practice Question: Below are a bunch of values, explain the memory region that each will reside in and why.
int globalVarA;
const char* globalVarB = "Hellooo Mrs. Clown, may I have a bowl of soup?";
void func() {
int localVarC = 42;
int* localVarD = new int();
}
int globalVarA;
const char* globalVarB = "Hellooo Mrs. Clown, may I have a bowl of soup?";
void func() {
int localVarC = 42;
int* localVarD = new int();
}
- A will be in the .bss section of Static memory since it is uninitialized,
but it will get a value of zero afterwards since globals are zero-initialized (unless they are of type auto).
- B will be in the read-only area of .data (the initialized Static memory section).
- C will be in Stack memory.
- D will be in Heap memory.
Additional reading:
https://www.geeksforgeeks.org/memory-layout-of-c-program/#
https://stackoverflow.com/questions/8721475/if-a-global-variable-is-initialized-to-0-will-it-go-to-bss
Caching
Caching is a process of optimizing memory usage to minimize how frequently we search main memory. Whenever your program asks the processor to bring it a section of memory, the processor brings a chunk of memory to a temporary storage location called a cache and then from that cache it returns the part you want. You can imagine it scooping up memory with imprecise mittens. The amount it moves at any given time is called a cache-line which is typically 64 bytes. When you ask it for memory again it will check if your newly requested data is within the recently scooped cache and if so it can bring you memory from there. If the processor can't find your data in the cache then it is considered a "cache miss" and it instead falls back to a very slow main memory load to find your data. It is extremely worthwhile to design our programs to reuse the same sections of memory again and again rather than relying on slow heap searches. That's because re-using data that is nearby each other in main memory increases the chance that it will all be scooped up together and stored in the cache.
Checkout this interactive demo which can help visualize the speed of obtaining cached data versus calling into main memory: Demo Link
Because reusing cached memory can leave to such amazing time savings, most computers are designed with multiple caches. If you played the demo linked above then you saw an L2 cache in addition to the smallest and speediest cache named L1. The basic idea here is the same, if we can't find data in the L1 cache, then check the L2 cache, and only after that do we fallback to a main memory look-up.
"Line size" refers to how many words fit in a cache line. On an x64 system we see a 1B word and a line size of 8, therefore we have a cache line size of 8B * 8 = 64B. Cache lines always access the same amount of memory and always access memory addresses on an interval of the cache line size. For example it may access the first 8B or the next 8B. It would never include something like bytes 2-10, because that is not on the 8B interval.
Checkout this interactive demo which can help visualize the speed of obtaining cached data versus calling into main memory: Demo Link
Because reusing cached memory can leave to such amazing time savings, most computers are designed with multiple caches. If you played the demo linked above then you saw an L2 cache in addition to the smallest and speediest cache named L1. The basic idea here is the same, if we can't find data in the L1 cache, then check the L2 cache, and only after that do we fallback to a main memory look-up.
"Line size" refers to how many words fit in a cache line. On an x64 system we see a 1B word and a line size of 8, therefore we have a cache line size of 8B * 8 = 64B. Cache lines always access the same amount of memory and always access memory addresses on an interval of the cache line size. For example it may access the first 8B or the next 8B. It would never include something like bytes 2-10, because that is not on the 8B interval.
Practice Question: If a program asks to grab the 10th byte of memory, what range of memory addresses will be accessed?
It will grab one cache line’s worth of memory starting at the next cacheline interval. On an 8-byte system (64-bit), the first interval would be indices 0 to 7. The second would be indices 8 to 15. So in total we would access bytes in indicies 8-15, pull those into the cache line, and return the 10th byte (which would be the second byte of our cache line).
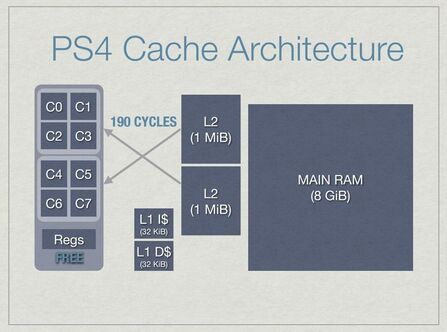
Below is a diagram from Jason Gregory's excellent talk Dogged Determination. In the diagram you can see the PS4 is designed with two groups of four CPU cores sharing an L2 and L1 cache each. The PS5 has an L3 cache as well, and some computers even have L4 caches.
Below is a diagram from Jason Gregory's excellent talk Dogged Determination. In the diagram you can see the PS4 is designed with two groups of four CPU cores sharing an L2 and L1 cache each. The PS5 has an L3 cache as well, and some computers even have L4 caches.
Be aware of the approximate size of the different caches you are dealing with on your target platform. Typically you will see an L1, L2, L3 then main memory. The difference between accessing each level is about 3 times slower. So main memory access is 27x slower than L1.
Practice Question: Let's consider the role of data locality in practice, below is a simple nested for-loop that traverses every element of a 2d matrix, we could choose option A or B to preform the desired ++ operation. Which is the faster option and why?
for (X = 0; X < MAX; X++) {
for (Y = 0; Y < MAX; Y++) {
Option A: arr[ X ][ Y ]++;
Option B: arr[ Y ][ X ]++;
}
}
for (X = 0; X < MAX; X++) {
for (Y = 0; Y < MAX; Y++) {
Option A: arr[ X ][ Y ]++;
Option B: arr[ Y ][ X ]++;
}
}
In this case, A is the faster option. It's faster because it is referencing consecutive values within the matrix. C and C++ store matrix values in row major order (https://www.codee.com/knowledge/glossary-row-major-and-column-major-order/ ) so that means when we grab a matrix index from memory it is going to come with a cacheline comprised of the other values in its row in addition to adjacent rows. We reduce the frequency of cache misses by primarily iterating through the rows of data recently cached rather than by primarily iterating through the columns which would have the processor jumping around memory and missing the cache more frequently.
Basically whenever you see a question like this (and I've seen them frequently in interviews) you want to look at the inner loop and make sure that variable is the one in the second part of the array index. For example if the loops were re-ordered (with Y as the outer loop and X as in inner) then Option B would be correct.
The question comes from the opening of Scott Meyer's "Cpu Caches and Why You Care" (you should definitely watch this lecture): https://youtu.be/WDIkqP4JbkE
Basically whenever you see a question like this (and I've seen them frequently in interviews) you want to look at the inner loop and make sure that variable is the one in the second part of the array index. For example if the loops were re-ordered (with Y as the outer loop and X as in inner) then Option B would be correct.
The question comes from the opening of Scott Meyer's "Cpu Caches and Why You Care" (you should definitely watch this lecture): https://youtu.be/WDIkqP4JbkE
In the above practice question we explored editing data in memory. However we are actually editing a copy of the main memory that has been cached (aka copied) into the L1 cache. The processor usually maintains a list of flags to track if cache lines within the caches have been changed and therefore determine if it needs to update main memory. The main memory update typically is handled when a cache's data is updated which only further extends the time cost of a cache-miss.
In a multi-processor environment, multiple cores can share the same cache; but if they affect its data, then they need to mark it as dirty which can lead to some nasty concurrency problems. To better support multi-processing, designs may include several caches of the same level. For example in the PS4 designs above, there are two L2 and L1 caches shared by four cores each. Likewise, processors can benefit from decoupling instruction storage into a separate cache so you might see those instruction-specific caches referred to by the term "i-caches" versus "d-caches" which are for data. Caches that are designed for both data and instructions are called unified caches.
In addition to reducing cache misses, applying cache locality principles to our program design can allow us to use powerful hardware operations called SIMD instructions. SIMD or "single-instruction-multiple-data" instructions allow us to to perform multiple computations at once. The exact capabilities of SIMD instructions are going to vary based on the hardware architecture, but getting down to the metal is what game programming is all about! Here is an example using SIMD for vector addition.
Additional terms to know:
- Cache-Thrash - when frequent cache misses require frequent loads from main memory.
- False-Sharing - when multiple cores are editing the same cache line and are frequently setting the dirty flag due to constant cache misses. This basically happens because when one process is grabbing memory for itself it is unfortunately scooping up a cache line that includes memory needed by another process. We will discuss this again in the future chapter on multithreading.
Practice Question: Let's imagine you are optimizing a game that manages thousands of player's where a player struct contains information described in the struct below. The game is currently designed with a huge array containing a struct instance for every player. In the game, we frequently need to cycle through that huge array to access all of the players' health and all of their positions to check things like who is dead or who is close enough to an exploding grenade to be affected. How could you apply the principles of data locality to this design to increase the speed of these operations?
struct Player {
int health;
Vector3 position;
string otherStringData;
}
struct Player {
int health;
Vector3 position;
string otherStringData;
}
This classic problem is often called an Array of Structs (AOS) versus a Struct of Arrays (SOA). In the answer they are looking for you to identify that iterating through the structs requires jumping over the other data which will result in far more cache misses than if the health floats were arranged beside each other. This problem will become worse if the player struct grows in size.This is just like the earlier problem where a column-major matrix traversal cost us to unnecessarily jump over rows of data.
The solution is to replace the array of structs with a struct of arrays like this:
Now we can iterate straight through all of health's values, performing the desired operations with far less cache misses. Additionally if we are performing the same operation on multiple values (such as decreasing all player's health by five points) then we now have the added affordance of using SIMD instructions because the data is contiguous.
The solution is to replace the array of structs with a struct of arrays like this:
struct Players{
int [] healths;
Vector3 [] positions;
string [] otherStringDatas;
}
Now we can iterate straight through all of health's values, performing the desired operations with far less cache misses. Additionally if we are performing the same operation on multiple values (such as decreasing all player's health by five points) then we now have the added affordance of using SIMD instructions because the data is contiguous.
The TLB (translation lookaside buffer) is an additional type of cache that maps addresses to virtual memory pages. When a computer runs out of RAM pages it can create virtual memory pages to simulate a larger memory capacity. However even though it can pretend to have a larger capacity, the RAM still has the same maximum storage capacity; so when it swaps out real pages with virtual pages it puts the real data into main memory and uses the TLB to remember where it put them. Here's a nice video demo of the process. Pages on a x64 system are all the same size of 4KB, but you can alternatively setup a TLB to segment virtual memory into non-uniformly sized allocations called segments; these two approaches are called paging and segmentation respectively.
Allocation
An allocator is an algorithm for partitioning memory for usage. Good allocators have high speed and low fragmentation. Fragmentation refers to inefficiencies in memory usage. There are two kinds of fragmentation:
The main steps of a basic "malloc" allocation are detailed in this video. In summary, they are:
Here are some common allocator designs; in an interview you will be expected to explain the designs of various allocators in addition to the benefits of each approach with respect to speed and fragmentation. Watch the lecture, Dogged Determination, from Jason Gregory for a brief primer on some of these designs. Keep in mind that for most allocators we are not cleaning the memory once it is freed, that takes too long. Instead we just record it as free and we write over it when the client requests the memory.
- Internal means giving a client more memory than they need, leading to wasted unused space within the allocations. It's like giving a very skinny man a super long bench all to himself, there is extra room on that bench that is wasted since the occupant is so skinny. (think: wasted space within allocated memory)
- External means you have memory available, but you can't allocate it because the free memory is interspersed between used memory causing it to be too small for the client to use. It's like telling a skinny person to sit in the center seat of a row of three seats; and then a fat 2-seat wide person wants a seat but even though you have two free seats, they are not contiguous so you can't fit the fat guy anywhere.
- There are many allocation strategies that you should be aware of below are some of the common approaches. As we learn about each approach we want to consider their limitations with respect to fragmentation. (think: wasted space between allocated memory).
The main steps of a basic "malloc" allocation are detailed in this video. In summary, they are:
- Determine the size of requested memory (including superclasses / vtables of a class if applicable)
- Enter a critical section for memory allocation
- Begin allocation logic (this varies but I explain a few common allocator designs below)
- If necessary, execute a system call to move the Break (to grow the heap). This requires a context switch from user mode to kernel mode.
- If necessary, the kernel may need to write to disk.
- The memory is returned and, back in user mode, the constructor is executed if applicable.
Here are some common allocator designs; in an interview you will be expected to explain the designs of various allocators in addition to the benefits of each approach with respect to speed and fragmentation. Watch the lecture, Dogged Determination, from Jason Gregory for a brief primer on some of these designs. Keep in mind that for most allocators we are not cleaning the memory once it is freed, that takes too long. Instead we just record it as free and we write over it when the client requests the memory.
- Slab allocator: Gives out "slabs" of memory but the size(s) of the slabs it provides are restricted. Usually slabs are all just one size but sometimes a slab allocator supports a very small range of sizes. Because the allocations have known sizes, they have known bounds which makes the allocator very fast to swap slabs in and out. However because we are rounded the requested memory amount up to the closest slab size, we are basically guaranteeing internal fragmentation for the benefit of having zero external fragmentation.
- Buddy allocator: first divides memory into big blocks that are then broken into smaller blocks that will be re-absorbed when they are freed. The sizes of allocation are somewhat arbitrary so external fragmentation chances are high. But there is less internal fragmentation than a traditional slab allocator.
- Stack AKA “LIFO” AKA "Ring" AKA "Bump" allocator: Used for situations that have predictable build-up and tear-down sequences. There is zero internal or external fragmentation since we know exactly what sizes are needed and that the memory allocation order will mirror the memory free order. Mind that we can grow the stack from two directions.
- Relocatable Heap: can move allocated blocks after deallocations, but it has to manually update any external pointers that were tracking addresses in the allocated blocks. This is useful if we want to extend an allocated object beyond the size we originally allocated for it.
- Pooled Allocator: gives small allocations but does not free until the pooled allocator is destroyed. Used for very many, very small, allocations but with short lifetimes. Similar to the stack allocator, we have very low internal fragmentation but this design allows us to reuse the allocated memory at the cost of some external fragmentation.
- Frame Allocator: A per-thread Stack allocator that gets wiped each frame.
- Static Allocator: Allocations are made at the start of the program during a defined setup window and then no further allocations are made throughout the duration of the program.
Practice Question: You require an allocation system that will allow for several AI to save data that they can refer to during their lifetime. There is a limit to the number of AI we plan to support but it will vary per level. There is a set amount of how much data each AI type will need but that amount varies drastically between the different types of AI. At the end of a level, all AI are destroyed. What allocator design would be a good fit for this scenario? Discuss the benefits and drawbacks of your selection with specific reference to both kinds of fragmentation that could occur.
Though there may be several viable approaches, I would choose to use a Stack allocator in this case. That's because I know the amount of data needed for each AI may vary drastically so I would fear that a slab allocator would require a conservative slab size that would lead to a lot of internal fragmentation. The stack allocator can provide a unique allocation size for each AI so we would have zero internal fragmentation. This approach does not allow us to re-size allocations but that is okay because there is a set amount of data that each AI needs. Because we do not know the order that the AI will die, when an AI dies that memory is no longer needed and deallocations will lead this design to have external fragmentation. However, since we have a limit to the number of AI in a level. We can anticipate the total amount of memory we may need and with this pattern we can choose to forgo deallocate memory after every AI death and instead wipe all of the allocated memory at the end of each level.
Unsorted Topics
i++ vs ++i
If the ++ comes before the variable then the value is incremented before it is accessed. If it comes after, then the value is accessed and incremented afterwards. We'll revisit this distinction in a later chapter concerning atomicity.
If the ++ comes before the variable then the value is incremented before it is accessed. If it comes after, then the value is accessed and incremented afterwards. We'll revisit this distinction in a later chapter concerning atomicity.
Practice Question: State the value of B and C after the following lines of code are executed:
C = 10;
B = C++;
C = 10;
B = C++;
The ++ comes *after* the value is accessed. So B is first assigned C's value of 10, then C is incremented. The final result is B=10 and C=11.
Version Control
Perforce is the industry standard for game development repository management. It would be helpful if you're familiar with the basics. This is a common question to discern a candidate's familiarity with the technology:
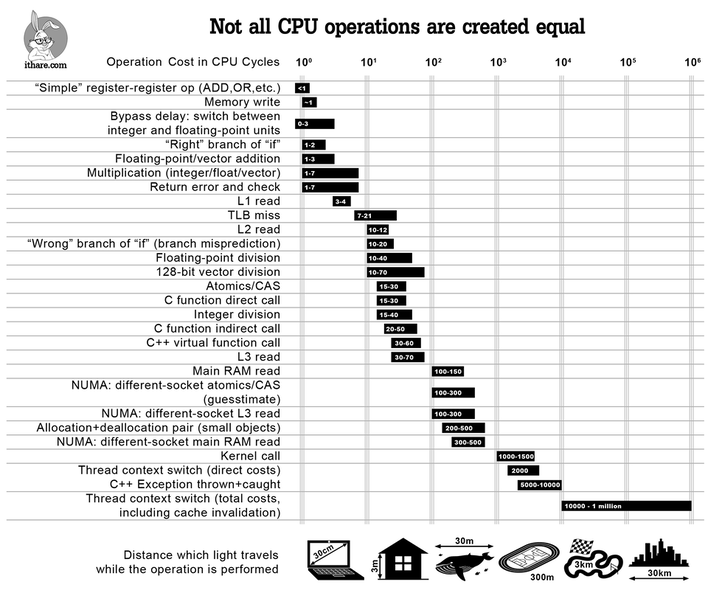
The following performance chart is useful for building an intuition between the relative costs of different CPU operations. You don't need to memorize anything here but you should know things like "multiplication is faster than division", "context switches are real bad", etc.
Version Control
Perforce is the industry standard for game development repository management. It would be helpful if you're familiar with the basics. This is a common question to discern a candidate's familiarity with the technology:
- Streams vs Branches LINK - Streams have privileged branches that “merge-down and copy-up”. Stream branches automatically receive changes from the mainline (OOO approach).
The following performance chart is useful for building an intuition between the relative costs of different CPU operations. You don't need to memorize anything here but you should know things like "multiplication is faster than division", "context switches are real bad", etc.